Answer to Quiz at Article #58:
There are several sources published in Pump Magazine on the subject of NPSH, which we recommend to review:
Article #1, “How Does
Pump Suction Limit the Flow?”
Article #3, “Suction
Specific Speed (Nss)
Quiz #1,
“NPSH and the Developed Head”
In simplest terms, a conceptual meaning of the available
NPSH (NPSHA) is that the total pressure at the pump inlet must be
sufficiently higher then the vapor pressure of the pumped liquid. If
not, the liquid will start transforming into its vapor phase, - not a good
thing for a pump! Positive displacement pumps community historically sticks
with pressure terms (such as psia, for example, in the
Thus: NPSHA = Hsuction,total – Hvapor
The required NPSH (NPSHR) is determined by the pump manufacturers via testing. NPSHA must be greater then NPSHR, plus some safe margin is desirable (see references above).
The total suction head consists of static (elevation) plus dynamic (velocity head), at the suction flange. However, many pump installations do not have a suction gage installed, and a pump inlet pressure is estimated by calculating friction losses between the feed tank and pump inlet, and subtracting these losses from the pressure (in terms of feet of head) at the tank surface.
The following should clarify this.
Say we have a tank open to atmosphere, which is 14.7 psia (absolute), or 34’ (if expressed in terms of feet of head). If the tank is filled with cold water 50 feet deep – the static pressure at the bottom is 34+50 = 84 feet. So far so good – basic hydraulics. And, we do not worry about dynamic head – if there is no flow, there is no velocity head. So, the total head is the same as static head for this case:
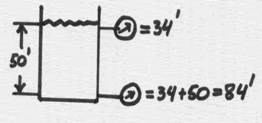
If we now weld-on a lid over the tank, nothing will change – 34 feet will still be at the top, and 84 feet at the bottom:
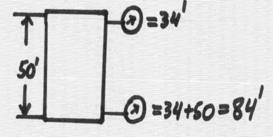
If we next install a pump between two tanks, this pump would have to do the work of developing a pump head (TDH = total dynamic head), to overcome the difference in liquid level between the tanks, which is 30 feet. The pressures at the surfaces of the tanks are atmospheric (tanks are open), so the pressure at the bottom of the small tank is 50’ higher, and in the big tank 80’ higher – as the basic hydraulics would require. So the pump would need to overcome that difference:
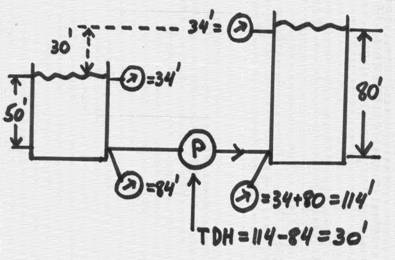
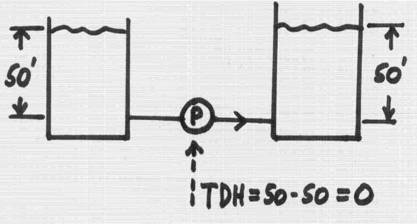
If the tanks are filled to the same level – there will be no differential pressure, and the pump, while working! – would have zero TDH. It will move a lot of flow – but at zero differential pressure. (By the way, this means that the pump operates at the intersection of its H-Q curve and the Q-axis).
Now, let’s take a look at the sketch below. The pump on the ground is pumping up on the roof, 50’ high. Instead of the two tanks we were just looking at, we now have a pipe on a left and a pipe on a right, - all connected. Let’s open valve “V” initially and have the system filled with cold water. The pressure at the valve junction is thus atmospheric, 34 feet. Same pressure is all along the horizontal section of a pipe on a roof, i.e. 34’.
Let’s next close the valve – and we got now “closed loop system”. Let’s also assume, for simplicity that the pipes have zero friction losses – as if they are short and polished to a mirror finish. Let’s also assume there is no heat exchanger installed yet – it will be delivered later! This way, for now, we can only deal with static head, and not worry about the friction losses.
When the pump starts, one thing it can not do is elevate the overall system level. In other words, the lowest pressure (34’) can not become, say, 40’ – the pump can not “pressurize its own suction” – the fluid circulating around would “chase its own tale” – as soon as the pump tries to compress some liquid by moving it to the left, the same amount of liquid comes toward the pump from another side, and makes room for the liquid displaced by the pump to move away – thus no overall pressure rise in a system. No wonder – this is a closed system!
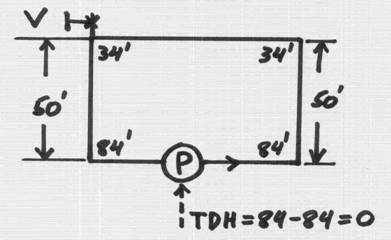
The pressure at the pump inlet is 34+50 = 84’ It is working hard, lifting the liquid from the ground floor to the roof, but the returning “downrunner pipe” keeps resupplying the liquid back to the pump suction. In other words, the horsepower is definitely not zero! – there is a lot of flow! – but at no pressure. Sounds kind of strange at first, but if you look at any H-Q curve at your pump catalogue – that is what happens (check it out!).
Now, what about the NPSHA? Well, since we pumping cold water, its vapor pressure is about 0.35 psia, or 0.8 feet of water. So, NPSHA = 84 – 0.8 = 83.2’
Next, let’s see what happens if we put the pump on a roof, instead of being on the ground:
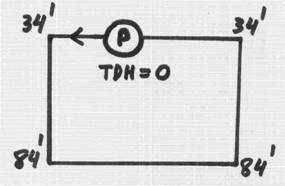
The pumping did not change – still zero TDH, but the inlet pressure is now lower by 50 feet – and the difference is – 50’ elevation. So, NPSHA = 34 – 0.8 = 33.2’
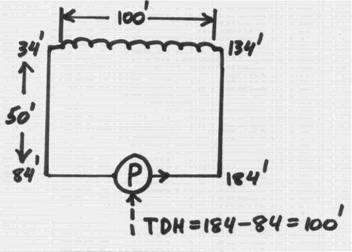
Now – the heater has arrived! – let’s plumb it in. Let’s assume its hydraulic passages are such that it takes 100 feet of pressure to overcome its restriction (pressure losses). Since we can not do anything with 34’ at the upper left corner, the result is just adding up numbers: 34+50 = 84’ at the bottom left, 34+100=134’ at the upper right to overcome the heater friction losses, then 134+50 = 184’ at the bottom right. And, what’s left for the pump is 194-84 = 100’ – to overcome the heat friction!
If the pump goes back up on the roof, it still has to handle the heater friction, but as far as its suction - it is again lower as compared to the ground position:
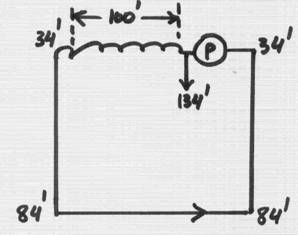
Let’s see what happens if the heater is on the side pipe that goes up to the roof from the pump:
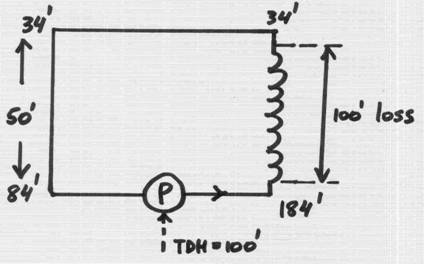
Above, TDH is the same, and the inlet head is 84’.
But, watch out for the heater at the bottom! – the drop across it must still be taken up by the pump head, and – we get a vacuum situation! - and, probably, cavitation:
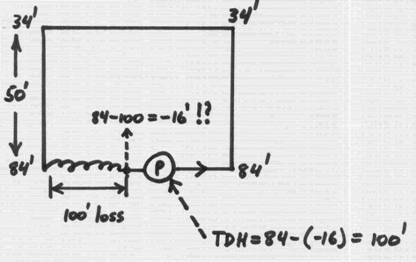
The moral of the story is – keep the pump at lowest elevation as possible, to take advantage of the hydraulics – higher pressure at the lower point. Also, do not clutter pump inlets with restrictions – heat exchanges, throttled valves, bends, small diameter or excessively long pipes, etc.
However, even though hydraulically not the best way, sometimes the pump may have to be at the higher elevation for other reasons – easier access, simpler maintenance, etc. If so, check what the NPSHA is, and – as long as it is sufficiently greater then the NPSHR – you may be fine, and so, hopefully, is a pump!