Article
#38: Newtonian and non-Newtonian Fluids.
Viscosity Effects on Centrifugal Pumps –
New Standard From Hydraulic Institute
(This
articles came out from the dialogue between our readers. Any additional input,
thoughts and questions are welcome)
Ed, -
I just wanted to let you know that the
Hydraulic Institute recently published a new standard to account for the
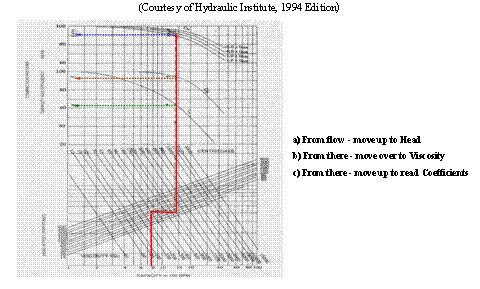
effects of viscosity of centrifugal pump performance. Previous to this method,
viscosity corrections were done using viscosity correction charts. I have not
read it yet since I just ordered a copy, but I thought some of you might be
interested in this new standard. Perhaps someone already looked into it and can
provide feedback.
The new
method is much easier to use because it calculates the viscosity corrections
automatically by using the formulas provided. There is no more need to
"eyeball" from charts, so the new method is more accurate. The
standard also provides a nice background description of the method as well as
its limitations and pump types and pump design characteristics for which
procedure is applicable. With the new method the efficiency corrections are
less severe as viscosity increases (hence less horsepower), but the flow and
head capacity corrections are a bit more severe. I would say the differences
between both methods are significant.
Question
for everyone, What is a pump with an
“essentially radial discharge”? And can I assume that crudes or refined
products behave as Newtonian fluids? These are some of the conditions in order
to use the new method.
Sergio Castellanos
Field
Technical Support
Chevron Pipeline Company,
Sergio,
Thanks
for the heads up.
Ed
Chevron
Serg, Ed -
I pulled out my old fluid mechanics book to bone up on
Newtonian fluids. I won't quote the definition entirely but a key statement is "The viscosity is a function only of the
condition of the fluid, particularly its temperature". Water,
oil, gasoline, alcohol and even glycerin are given as examples of Newtonian
fluids. Examples of non-Newtonian fluids given were slurries, suspensions, gels
and colloids. I would feel comfortable with the assumption for crude and
refined products. But I must ask the question: does heavy crude, or at what
point (low temperature), stop behaving like a Newtonian fluid? But I think at
all pumpable temperatures, crude is a Newtonian fluid.
The radial discharge question is a
bit tougher. As we discussed, I believe it is referring to a typical end
suction or open face impeller where the fluid is discharged perpendicular to
the shaft centerline or suction direction. Perhaps they are highlighting that
the method does not work for axial flow centrifugals (turbine pumps) where the
impeller side walls are angled beyond 90 degrees and /or propeller type pumps.
I am forwarding this to Dr. Lev
Nelik, with whom I have worked in the past, as he may have some insight on all
of this and may be familiar with the Hydraulic Institute publications.
Charles Lyons
Chevron,
Engineering Technical Services
Charles, -
Most of the fluids are Newtonian, with basic
definition being that viscosity is constant with the shear rate. What is shear
rate? It is relative stress imposed on fluid by the moving fluid. Consider, for
example, a 10” OD closed impeller, with 0.010” radial clearance between
the wear rings which are at 5” diameter. If it rotates at 3600 rpm, then the
metal peripheral velocity is 78 ft/sec (you can calculate this). The fluid in
direct contact with the ring is spinning at the same velocity, according to a
so-called no-slip condition. The stationary ring is 0.010” away from the
moving, so the gradient of velocity is (78 – 0) / (0.010/12) = 94,300 ft/sec /
ft = 94,300 1/sec – and that is what the shear rate is.
For an open impeller, the distance (“du”
component in formula – see graph below, which shows a formula for shear stress
as a product of viscosity times shear rate) is between the spinning impeller’s
open vane and the casing wall. Now the peripheral velocity changes along the
radial position of the vane (it is less at 5” as compared to the OD of, say,
10”), but an average value can be estimated (calculation is similar to the
above), and the shear rate will be similar.
Shear-sensitive fluids do not like such
shearing action. Glue, for example, gets “gooked-up” , as you would intuitively
imagine. Glue, however, is not pumped by centrifugal pumps, bit more typically,
by gear pumps. Shear rate, however, still works there as well: in a clearance
between the spinning gear and the wall, and such clearance is also typically in
the range of 0.005” or so.
Such shear rate, however, is usually not an
issue, as the amount of product in the clearance is small, and the overall
“dilution” by the gooked-up damaged fluid is negligible. But in certain cases,
it does matter. For example, if the fluid pumped by a gear pump is an emulsion
deposited on a Kodak film, then even minor imperfections may cause specks and
blemishes, and thus film strip ends up bad.
Similar concerns are for pumping food
stuffs, such as cherries, applies, etc. in canned food industry, and the pumps
requirement is gentle pumping, with low shear. Progressing Cavity pumps work
best for those cases.
Going back to centrifugals, the gap between
the impeller wall and casing wall is big – perhaps 0.5” or so, - thus shear
rate, for the example we use here, is (78 – 0) / (0.5/12) = 1870 1/sec
Now, for Newtonian fluids viscosity does not depend on the shear rate. If
your pumped oil has 300 cSt viscosity, for example, it stays so at 3600 rpm
pump, or 1800 rpm pump: shear rate changes, but viscosity is still 300 cSt.
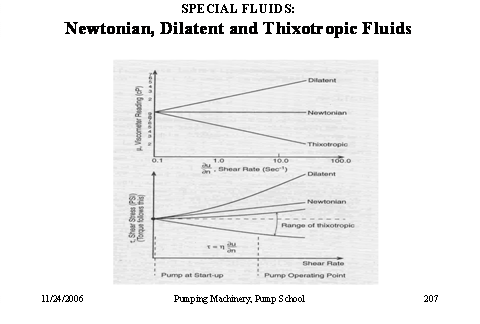
But for some fluids viscosity does change –
either up, or down, as shown on the chart, and such fluids are called Dilatent
or Thixotropic. This has an effect on power required, and also may cause fluids
degradation, in addition to having an effect (and usually does) on power. Power
is force times speed. Force is stress times area. Stress is viscosity times
shear rate –and so here we are. For
dilatent fluids shear stress goes up always, as both viscosity and shear rate
increase, but for thixotropic fluids it can go either way: shear rate may not
increase as fast as the decrease in viscosity, and the product (stress) can
increase, decrease, or stay about the same. It all depends on a specific fluid
being pumps. Usually, however, shear stress decreases. That means that power to
the pump also decreases with shear rate – in other words, fluid is first
viscous but once it starts moving it becomes less viscous which means less
power to pump it. It is common to neglect the driver rating (motor selected too
small): it gets sized per viscosity of the fluid in motion, but then a motors keeps tripping upon start-up! - as it
takes (much) more power to get things going. Ketch-up you use for your hamburger is such example – and this is
why you shake the bottle like crazy at the restaurant, to get it flowing
but once it flows – it does so quickly – (and all over your shirt!)
Below is a slide on this subject from the
notes of my
On
left (from
Also, I agree that a formula for viscous
correction is easier to use as compared to the previously published (also useful)
correction charts, and Hydraulic Institute has excellent information via their
standards and it is a good idea to have a set for practicing engineers that
deal with various pump issues and methods.
Dr. Lev Nelik, P.E., APICS
Editor
Pump Magazine On-Line