ARTICLE #13: PARALLEL OPERATION OF CENTRIFUGAL PUMPS
and the Importance of Curve Stability
Some time ago, one of our readers asked a question
about a parallel operation of pumps. This prompted a discussion which was
posted under Q&A Section, Question #25. Later on, another reader
inquired about the unstable curves and their effect on pumps parallel
operation, which resulted in another Pump Magazine Article (#8).
This generated interest from our friends at Pump-Flo company, who asked our
permission to reprint the article on their web site. Pump-Flo is a maker of
pump hydraulic selection curves program, for the pumps made by several pump
manufacturers. Their readers also liked the topic on parallel operation, and
more discussion followed, which we posted in Q&A Section, under Question #48.
We have been
receiving more questions and comments from our readers, and the latest one
(which we show below) convinced us of a need to respond with a formal article
(#13), which is what you are reading.
Question:
A chemical pump supplier engineer was asked why two of his
pumps in parallel appeared to be unstable at certain points on the curve,
notwithstanding that the curve was an inherently stable curve with continuous
rising gradient to shut off. Both pumps are identical, same diameter impeller,
end suction type.
This instability was experienced in a mining plant on a
cooling tower system with acidic water at 50 deg C. The instability could be
corrected by altering the settings of the discharge gate valve, i.e. changing
the head and flow on the pump. The suction head was more than adequate at 10
psig. The NPSHr was less than 0 psig.
His explanation was linked to the suction manifold, which
directed liquid in a straight feed to one pump [A] and liquid via 2 x 90 degree
elbows to the second pump [B]. There was a very short straight portion of pipe
between the 2nd elbow and the suction flange on pump B, approximately 3-4 pipe
diameters [pipe dia 10"]
This arrangement it was argued, caused the suction head on
the 2nd pump to fluctuate rapidly, both increasing and decreasing the suction
head to pump B beyond the smooth flow suction head experienced by pump A. This
fluctuation or vortexing could be substantial enough to cause the 2 pumps to
fight themselves and result in the instability experienced.
While the argument is plausible and credible, is this a
recognized phenomenon in the industry that can and has occurred on a number of
other occasions? The solution, if this is the cause of the instability, would
be of course to change the manifold to more smoothly direct flow to the 2nd
pump, eliminating the 90 degree elbows.
Hugh Lloyd
National Process Equipment,
Answer:
Dear Hugh,
As we understand it, this is a setup you have:
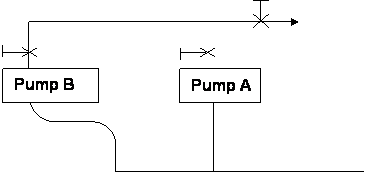 V3
V3
![]()
![]() V1 V2
V1 V2
EL2
EL1
Note: elbows EL1 and EL2 are shown within the
same plane for sketch simplicity, but in reality most likely are in different
planes.
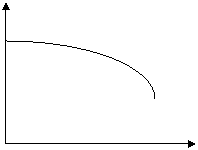
The “stable” curve the supplier engineer pointed to is
probably a manufacturer curve from the catalog, which probably looks something
like this:
 Head
Head
Flow
The H-Q curve is “continuously rising”, i.e. deemed
stable.
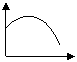
Pump Magazine Article #8 talked about unstable
(“drooping”) curves:
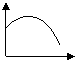
H
Q
As was explained in Article #8, unstable curves cause
problem for pumps operating in parallel, which would explain Hugh’s problem.
However, what is puzzling is why the two pumps, having stable curves, behave as
if their curves are unstable?
However, the pumps are not identical. Clearly,
the suction approach to Pump B is different from Pump A. While it is generally
known that sharp turns, multiple elbows, short pipes, and other obstructions
are not a good thing for pumps, and
numerous Case Histories have been published to illustrate and warn the pump
users not to do that (Hydraulic Institute even issued guidelines on suction
approach dimensions, sump configurations, etc. – all to help avoid problems) –
questions nevertheless come up each time another problematic parallel operation
surfaces.
There are many reasons why “tipsy-turvey” suction
could cause instability. Let’s take a look how an apparently “stable” H-Q
curve, even as tested by the manufacturer, can become “unstable” when a pump
ends up with a “curvey” suction. There is no other way to understand this
without having to delve into the heart of the impeller hydraulics. The head
generated by the impeller is the difference between the velocity angular
momentum between the impeller inlet and exit:
H = [ (U x Vtheta)OD
- (U x Vtheta)eye ] / g
 Impeller
OD
Impeller
OD
Impeller Eye
![]()
The “g” is
gravitational constant, U is peripheral rotational velocity, subscript “theta”
means “peripheral projection of the absolute flow velocity vector”, and H is
impeller head. If fluid velocities are taken in feet per second, and g=32.17
ft/sec2, then head H comes out in feet. There is also hydraulic
efficiency involved, but we skip that for simplicity.
Hydraulic designers refer to this in terms of
“velocity triangles”, which essentially is a set of fluid velocity vectors are
the inlet and the exit of the impeller:
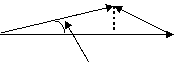
![]() W1 V2 W2
W1 V2 W2
V1
U1 U2
Alpha1 = 90 degrees Alpha2
= 20 degrees
The projection of the
absolute velocity “V” onto peripheral velocity “U” is called Vtheta .
For most end-suction pumps, the
absolute flow angle at the inlet is 90 degrees, which is also referred to as
“no-prewhirl” condition. Thus the projection of the “V1” velocity onto “U1” is
zero, and thus the product (U x Vtheta)eye = 0
For example, if a Pump
A develops 100 feet of head at the BEP point of 1000 gpm, the impeller exit
component contributes all 100 feet if there is no pre-whirl, and there is no
effect of the impeller inlet – no addition and no subtraction. At lower flow,
the exit velocity triangle changes (Vtheta)OD component
gets larger, and thus more head is generated. At the shut-off, there is no
through-flow, and the (Vtheta)OD essentially overlays
directly over the vector “U2”. Thus, at zero flow (shut valve), the head is the
highest, - for typical end-suction pumps, such as ANSI, for example, the “rise
to shut-off” is approximately 110 - 130%.
And in order for the H-Q curve to be “stable” this rise must be
“continuous” – in order to avoid instabilities if operated in parallel.
Double-suction pumps,
for example, are different. Their casing forms a “toilet-bowl-shaped” suction,
which – just as a toilet! – creates a prewhirl:
![]()
U1
Alpha1
= 45-60 degrees
Now the product (U
x Vtheta)eye is not
zero! If this product amounts to, say, 30 feet, the impeller would generate
less head: 100-30 = 70 feet. However, hydraulic designers would compensate for
that by altering the impeller exit geometry – width, blade angles, etc. – so
that the exit portion would produce extra head, say 130 feet – and the net
result would remain the same 130-30 = 100 feet.
Therefore, by changing
impeller geometry, it possible to change the curve shape, including the rise to
shut-off. Likewise, by changing the pre-rotation (pre-whirl), it is also
possible to change the rise-to-shut-off. In fact, the change could go either
way – the head at the BEP can either increase, or decrease – depending whether
the pre-rotation is positive (as shown above), or negative. The shut-off head,
however, does not depend on prerotation component.
When a designer
accounts for a known pre-rotation in the casing (such as for double suction
pumps example), he or she does it in a way to preserve the flow dynamics, and
maintain smooth flow and good efficiency. The designer has not control,
however, if the pre-rotation is created artificially, such as bad suction
piping, multiple elbows, and so on, -
including the direction of the prerotation. If the “deck gets stacked the wrong
way”, the flow in the suction piping may end up with negative rotation, - and
double-turning elbows are known to be nasty on flow patterns.
The resulting velocity
inlet triangle may thus look like this:

Alpha1 = 140 degrees, i.e. negative
Vtheta results.
This could create a
negative inlet term - for example, (U x
Vtheta)eye = - 40 feet (minus). Since the exit is fixed,
the net head would become 100 – (-40) = +140 feet, - which is obviously greater
then the shut off head, - i.e. an unstable curve got created:
 Hpeak=140
Hpeak=140
Hso=
120
Q
As Hugh rightly noted, the solution, if this is the
cause of the instability, would indeed be to change the manifold to a more
conventional and appropriate inlet piping configuration. Even though there
could always be other reasons involved, a good piping is not a guarantee, but a
beginning to a trouble-free pump operation.
Next, let’s look at the
parallel operation in more detail, starting with stable curves.
Situation 1: Single Pump

The pump must generate
pressure (head) to overcome hydraulic losses in the system. These losses
consist of losses in a valves, bends, elbows, heat exchanger and pipe friction.
From basic hydraulics, a friction loss is proportional to the square of flow:
HLOSS = k x Q2
The
summation of individual losses is equal to a total system hydraulic loss:
HLOSS
= KVALVE X Q2 + KELBOW X Q2 + KHE
x Q2 +… = (KVALVE + KELBOW + KHE
+…) x Q2 = kSYSTEM x Q2
We were
able to do the math above and add the individual hydraulic coefficient due to
the fact that the flow is the same throughout the system. We could not do that
so easily if the system had branches, with flows branching out all over. This
is analogous to the electric circuit, where the same current flowing from one
component to the next result in different voltage drops across the individual
resistors. In hydraulics, the pressure drop due to fluid flow is similar to the
voltage drop due to electric current.
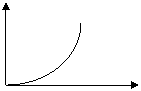 Once the kSYSTEM is calculated,
a system curve can be
plotted: hLOSS
Once the kSYSTEM is calculated,
a system curve can be
plotted: hLOSS
Flow
If the pump curve and a
system curve are plotted together, an intersection thus determines the pump
operating point, because it belongs to both curves:
Head

Flow (Q)
Situation
2: (2) pumps in parallel, but with a common resistance element (valve)
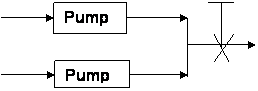
Flows
Q1 and Q2 combine, and that is what flows through the valve: Qvalve = Q1+Q2
The
valve curve is similar parabola as shown in the previous example:
h = k x Qvalve2 = k x (Q1+Q2)2
Mathematically,
a pump curve is a Head as a function of Flow. Or, it can be also expressed as
Flow as a function of Head, i.e.:
Q1 = f(H1), and Q2
= f(H2)
In
general, the pumps do not have to be identical.
Then,
Qtotal = Q1+Q2 = f(H1) + f(H2)
Since
Qtotal = Qvalve, the combined pump curve and a valve (i.e. system) curves can
be plotted and the intersection would determine the head (pressure) where the
pump/system will operate:

Head
1 pump 2 pumps (Qtotal = Q1 x 2)
500 600 Flow, gpm
(for simplicity both pumps here were
assumed to be identical)
Note
an interesting thing: when only one pump was operating (point “500 gpm”), the
flow was 500 gpm. But when the second pump also came on line, they together,
did not produce 500x2 = 1000 gpm! Instead, only 600 gpm flows through the
system! Clearly, the answer to that is in the shape of the system resistance
curve. However, if the pumps were pumping against mainly a static head (such as
pressurized tank) – then the flows would be additive! Why? Because the
static head curve is not a parabola, but a straight line, independent of flow,
and thus parallel to the flow axis:
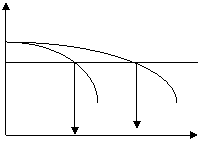
Head
100 psi (system)
500 1000 Flow, gpm
500 gpm 1000 gpm
100 psi
500 gpm
Note:
in general, a combination of friction as well as static heads may be present,
although usually either one or the other scenario is more predominant.
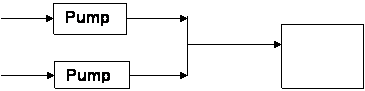
Situation
3: (2) pumps in parallel, but NOT with common resistance
Now,
that is getting interesting. In the previous example, the change of the valve
setting (changing valve “k” coefficient) affects both pumps the same way. But
what if we have a system like this:
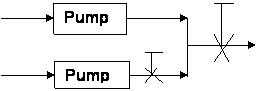
Common valve, V0
Valve V2
Let’s
assume, for simplicity, two identical pumps, and the valves are identical also.
Assume also that each valve is throttled the same percentage (i.e. having the
same coefficient “k”):
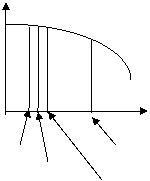
Head,ft PUMP CURVE hsys
(Hso=
120 ft)
HBEP =
100 ft VALVE CURVE
Flow, gpm
Flow, gpm
250 500 (BEP)
300
400
Digitize
several points form the valve curve into a Table below to make it easier to
work with, as we go:
|
Flow, gpm |
100 |
200 |
300 |
400 |
500 |
600 |
|
hsys, ft |
4 |
16 |
36 |
64 |
100 |
144 |
We
know the following:
![]() Assume there are no other losses except
for the (2) valves. In other words, all other losses have been combined into
the (2) “equivalent” valves V0 and V2
Assume there are no other losses except
for the (2) valves. In other words, all other losses have been combined into
the (2) “equivalent” valves V0 and V2
![]() Valve V0 sees the combined flows: from
Pump 1 plus Pump 2
Valve V0 sees the combined flows: from
Pump 1 plus Pump 2
![]() The head generated by the Pump 1 is
equal to the pressure drop (head loss) across the Valve V0, because of the
pressure continuity – the nodal point at the exit of the Pump 1 is the same as
the entry point into the Valve V0
The head generated by the Pump 1 is
equal to the pressure drop (head loss) across the Valve V0, because of the
pressure continuity – the nodal point at the exit of the Pump 1 is the same as
the entry point into the Valve V0
![]() Valve V2 sees flow from Pump 2 only
Valve V2 sees flow from Pump 2 only
![]() System must be in balance, to satisfy
individual pump H-Q curves, and individual valve h-Q curves.
System must be in balance, to satisfy
individual pump H-Q curves, and individual valve h-Q curves.
The
solution is iterative:
a)
Guess
at the flow from Pump 1, Q1=250 gpm.
b)
Per
H-Q curve of Pump 1, head H1=118 feet
c)
Head
loss across valve V0 is equal to head generated by Pump 1, i.e. valve h1=H1=118
ft
d)
From
the valve V0 curve, Q0 = 543 (we actually “cheated” a bit here – got the
equation for the parabola, h0 = Q02/2500, and then just plugged-in
the numbers)
e)
Total
pumps flow is equal to what is flowing through valve V0, i.e. Qtotal=Q0=543
f)
Flow
through Pump 2 is the difference: Q2 = Q0 – Q1 = 543-250 = 293 gpm
g)
From
the Pump 2 curve (we used identical pumps in this case), H2 = 116 ft (approximately,
as it is more difficult to derive the polynomial equation for the pumps. For
the valve it is easy - parabola)
h)
A
pressure drop across the valve V2 is the difference between the pressures at
its exit and inlet. The exit pressure is equal to what Pump 1 generated, and
the inlet is what Pump 2 generated, i.e. h2 = 116-118 = -2 ft. This is
impossible, i.e. our first guessed flow from Pump 1 was wrong. Let’s re-guess
and go around again:
a)
New
guess, Q1=300 gpm
b)
H1
= 115 ft
c)
h0
= H1 = 115 ft
d)
Q0
= 536 gpm
e)
Qtotal
= Q0 = 536 gpm
f)
Q2
= Q0 – Q1 = 536 – 300 = 236 gpm
g)
H2
= 119 ft from pump curve
h)
h2
= H2 – H1 = 119-115 = 4 ft
i)
From
valve curve (or interpolating from the Table), Qvalve2=100 gpm
j)
Q2
= Qvalve2 = 100 gpm (from the flow continuity – what flows to Valve 2 has to
come out from Pump 2). This is not equal to Pump 2 flow as derived at step (f),
so we need to guess again. (But we are getting closer).
a)
Next
guess, Q1 = 400 gpm
b)
H1
= 113 ft
c)
h0
= H1 = 113 ft
d)
Q0
= 532 gpm
e)
Qtotal
= Q0 = 532 gpm
f)
Q2
= Q0 – Q1 = 532-400 = 132
gpm
g)
H2
= 119.5 ft from pump curve
h)
h2
= H2 – H1 = 119.5-113 = 6.5 ft
i)
Qvalve2
= 127 gpm
j)
Q2
= Qvalve2 = 127 gpm
We
now reached a reasonable convergence. Thus the final answer is:
Pump
1: flow = 400 gpm, head = 113 ft
Pump
2: flow = 132 gpm, head = 119.5 ft
The above solution has a numeric (analytical) counterpart, and could be
solved by writing a set of simultaneous equations and solving them:
h2 = k2 x Q22
h0 = k0 x (Q1+Q2)2 – we could even have
different valves or valve settings (different k0 and k2)
H1 = f(Q1) or Q1 = f(H1)
H2 = f(Q2) or Q2 = f(H2) – pumps also could be
different
H1 = h0
h2 = H1 – H2
(6) equations and (6) unknowns: Q1, Q2, H1, H2, h1,
h2
Clearly, even a simple case of just two
pumps and two valves can be a rather time consuming task to solve.
Clearly, for a real pumping system, with many pumps and components, a manual
method is impractical. This is when computers come handy, as Ray
Hardee P.E., Engineered Software, Inc, explained in the discussion for Question
#48. Obviously a more refined math and methods can be employed – but let’s
leave that for the programmers and mathematicians! For now, and from the
practical point of view, - if we have a piping network program like that and a
clear manual of how to use it – a solution of even a complex system would
become an easy job.
One of such companies is Sunrise
Systems, and you can get more information about them and
their product via their web site at www.sunrise-sys.com
Note that we have only touched on systems with stable
curves. What happens if the pump curves are not stable? Well, mathematically,
we get multiple solutions. In other words, just as was explained in Article #8,
a pump would be technically able to operate at two flows – for the same given
head. How do programs like the ones mentioned solve this?! That, however, is
another issue. In the meantime – stay away from the unstable curves, and, for
that matter – from bad piping!
Keep on pumping!
Dr. Lev Nelik, P.E., Apics
Pumping Machinery
Note: if you would like to learn more about pumps,
systems, theory, as well as hands-on pump reassembly work – come to our next
We welcome your comments to: